A Bayesian approach for estimating the uncertainty on the contribution of nitrogen fixation and calculation of nutrient balances in grain legumes | Plant Methods

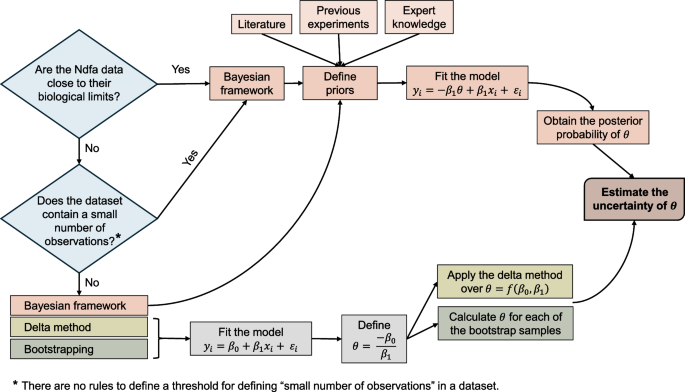
We illustrate the three methods (delta method, bootstrapping, Bayesian inference) for quantifying the uncertainty on \(\theta\) by retrieving the data from [13]. The workflow implemented in this study is depicted in the flowchart presented in Fig. 2. Furthermore, Fig. 2 provides information to future users to decide in which cases apply the Bayesian framework developed in this article. Since there is no rule for defining when datasets are small, overall, it would be justified running the proposed Bayesian framework in cases where information is available to define priors and/or the delta method and/or bootstrapping provide unreliable uncertainty estimations (e.g. \(\theta >100\%~or~\theta <0\%\)).

Flowchart depicting the workflow implementing in this study and showing the cases where it is worth applying the developed Bayesian framework

Data collection and description

The variables (Ndfa, fixed N, seed N) were collected in chickpea (Cicer arietinum L.), common bean (Phaseolus vulgaris L.), cowpea (Vigna unguiculata L.), faba bean (Vicia faba L.), field pea (Pisum sativum L.), lentil (Lens culinaris Medik), white lupin (Lupinus albus L.), blue lupin (Lupinus angustifolius L.), and peanut (Arachis hypogaea L.). A similar literature search was conducted to retrieve the proportion of N that is allocated to the roots and rhizodeposition with respect to the total N in the plant (above + belowground N). For more details about the criteria to select papers for the database see [13]. We also included unpublished data for peanut in the current study.

Variable descriptions and calculations

The authors in [13] studied belowground N contributions retrieving the information from articles implementing physical recovery and ¹⁵N-labelling techniques for quantifying belowground N [15]. With the collected information, Palmero et al. [13] calculated a root factor as:

where Below ground N and Above ground N refer to the proportions of N found below and above the ground, respectively, relative to the total plant N demand. For instance, assume a scenario where the total N in a crop (considering above and belowground structures) is 125 kg ha⁻¹, but this value is unknown. What is known is the amount of N (kg ha⁻¹) in the aboveground structures of the crop and the proportion of N allocated to the roots relative to the total N in the crop. Assuming that the aboveground N is quantified at 100 kg ha⁻¹ and the root N allocation is 20%. Therefore, we know that 100 kg of N ha⁻¹ represents 80% of the total N in the crop. Therefore, by calculating the root factor, and applying it to estimate the total N uptake (above + belowground structures), we have the following:

Thus, the root factor allows the incorporation of the N allocated to the roots when calculating the total fixed N by a crop (see Eq. 5).

The Ndfa (%) values, representing the proportion of total aboveground N derived from the N fixation process, were obtained through a literature review only for aboveground parts of the crop. The fixed N (kg ha⁻¹) can be calculated by excluding the contribution of N from roots and rhizodeposition as follows:

In addition, assuming Ndfa did not differ between above- and below-ground structures [16], the Ndfa estimated for the aboveground tissues can be used to estimate the fixed N considering the belowground N contribution according to Eq. 3 and Eq. 4 as

Lastly, the Fixed Aboveground N and Total Fixed N can be used to calculate the PNB and TNB, respectively, as follow:

If either of these balances are positive, it means that the fixed N (excluding (Eq. 6) or including (Eq. 7) belowground N contribution) is greater than the N exported in seeds and a net soil N input occurs, resulting in a positive N balance. On the other hand, negative values indicate that the fixed N was not enough to compensate the N exported in seeds and a net soil N reduction takes place, resulting in a negative N balance.

Statistical models

In this section, we will provide details about the different approaches to estimate the parameter of interest and introduce a few modifications in the original model [7, 8] to incorporate previous knowledge in the statistical model.

Regression model

First, we used a simple linear regression model for PNB or TNB as a function of Ndfa. We introduced this model in Eq. 1 as

where \({y}_{i}\), \({x}_{i}\), \({\beta }_{0}\), \({\beta }_{1}\), and \({\varepsilon }_{i}\) have the same interpretation than that mentioned in the background section for Eq. 1. This model has a deterministic part, \({\beta }_{0} + {\beta }_{1}{x}_{i}\), and a random part, \({\varepsilon }_{i}\), which is usually assumed that \({\varepsilon }_{i}\sim N(0, {\sigma }^{2})\). The Ndfa needed to achieve neutral N balances in grain legume species (called \(\theta\)) can be calculated as a function of \({\beta }_{0}\) and \({\beta }_{1}\). The delta method and bootstrapping can be implemented to quantify the uncertainty of \(\theta\).

The delta method allows us to approximate sampling distributions for functions of random variables. Since both \({\beta }_{0}\) and \({\beta }_{1}\) have their own variance estimation and \(\theta\) is a function of the \(\beta {\prime}s\), the delta method can be applied to estimate the variance of \(\theta\) [17]. Then, under the assumption that the sampling distribution of the ratio \(\frac{-{\beta }_{0}}{{\beta }_{1}}\) is asymptotically normally distributed, the approximated variance of \(\theta\) (obtained via delta method) can be used to construct confidence intervals.

The bootstrapping technique utilizes the plug-in principle to estimate the population distribution based on the empirical distribution of the observed data [10]. Applying this computational technique to a linear model consists of taking K random samples (with replacement) of the same size as the original data (n), and then fitting the linear model to each of the K samples of size n. Finally, the K estimates are utilized to construct the confidence interval of \(\theta\). In this study, K was equal to 10,000.

Bayesian inference

Bayesian inference offers an alternative to solve the challenges found when implementing the delta method and bootstrapping for this particular study. Through Bayesian inference, the estimation of the model parameters and their variability can be regularized by including previous knowledge into the model [18]. For example, in Fig. 1, values of \(\theta\) greater than 100 are not possible. Therefore, it is realistic to incorporate this assumption into our linear regression model. Up to this point, the model as presented in Eq. 1 can be implemented under any framework. However, a Bayesian framework is needed in some situations because it allows us to incorporate information about the model parameters in the form of probability distributions, known as prior distributions (regulator; Table 1).

As described, the regression model in Eq. 1 does not allow to incorporate knowledge about the \(\theta\), because \(\theta\) is not directly but indirectly present in Eq. 1 by utilizing \({\beta }_{0}\) and \({\beta }_{1}\) (Eq. 2; Fig. 1). In Bayesian inference any unobserved quantity is considered a random variable. Therefore, the model parameters \({\beta }_{0}\), \({\beta }_{1}\) are random variables under the Bayesian paradigm. Furthermore, a function of a random variable is also a random variable. We showed that \(\theta = \frac{{-\beta }_{0}}{{\beta }_{1}}\). Therefore, \(\theta\) becomes a parameter that models the proportion of N that the legume crop has to fix (Ndfa) to achieve a neutral N balance. Using the expression \(\theta = \frac{{-\beta }_{0}}{{\beta }_{1}}\), we can write \({\beta }_{0}\) as a function of \(\theta\) and \({\beta }_{1}\) represented as \({\beta }_{0} = {-\beta }_{1}\theta .\) Now, we can use the last equality to plug it in Eq. 1. Thus, the original linear model can be re-written as

where \({y}_{i}\) is the PNB or TNB (kg ha⁻¹) for the ith observation, \({x}_{i}\) is the ith observation of Ndfa, \({\beta }_{1}\) represents the change in PNB or TNB per unit of Ndfa, \(\theta\) is the Ndfa required to achieve a neutral N balance, and \({\varepsilon }_{i}\) is the residual error. Since the framework we propose in this study is Bayesian, we need to provide priors (also called parameter models) for the model parameters in Eq. 8. We have assumed that \({\varepsilon }_{i}\sim N\left(0, {\sigma }^{2}\right).\) Therefore, \({\sigma }^{2}\) ─or the standard deviation (\(\sqrt{{\sigma }^{2}}=\sigma\))─ is a parameter to be estimated as is \({\beta }_{1}\) and \(\theta\). The parameter models (priors) selected on this study were:

The numerical values within the parentheses in Eq. 9–11 are the parameters that shape the probability distribution. In Bayesian inference, these parameters (e.g., 1.6 and 0.8 in Eq. 9) are referred to as hyperparameters (Table 1). In this study, we uniquely determined the values for the hyperparameters for the beta distribution (\(\alpha\) and \(\beta\)) for each species, and their values are presented in Table 2. Setting the hyperparameters allows us to define the expected value and variance for the prior probability distributions. The computed expected values were \(E\left({\beta }_{1}\right)=\frac{1.6}{0.8}\), \(E\left(\sigma \right)=\frac{2.5}{0.05}\), and \(E\left(\theta \right)= \frac{\alpha }{\alpha +\beta }\). More details related to parameters and probability distributions selected as prior are provided in the subsequent sections.

Informative priors

The Bayesian framework consists of three core steps: (i) determining the likelihood function; (ii) capturing the knowledge about the parameters in the statistical model through the prior distribution; and (iii) combining the likelihood and the prior applying the Bayes’ theorem to obtain the posterior distribution of the model parameters (Table 1; Supplementary Note 1). The priors influence the posterior distribution of the model parameters, as the posterior is a balance between the data, the likelihood, and the priors [19, 20]. However, the impact of the priors on the posterior is usually reduced as sample size increases. Bayesian statistics allow us to incorporate previous scientific knowledge into our model through the use of priors. The information (data or expert knowledge) used for specifying the hyperparameters must be independent from the data used to fit the parameters of the model [18]. In this study, we employed informative priors for the model parameters based on independent information collected from previous studies.

Because a greater Ndfa means a larger proportion of the total crop N being fixed, higher Ndfa results in larger N balances, making \({\beta }_{1}\) to take positive values [7, 8, 14]. The standard deviation parameter (\(\sigma\)) is the positive square root of the variance, and thus, can take only positive real numbers. The gamma distribution is a continuous distribution of the positive real numbers that can take different shapes. Therefore, we chose the gamma distribution to represent our prior knowledge of \({\beta }_{1}\) and \(\sigma\). The parameter \(\theta\) represents a proportion, indicating the Ndfa required to achieve a neutral N balance. Therefore, \(\theta\) can take only positive values between 0 and 1 (or 0 and 100 if scaled). Since the beta distribution models continuous random variables that can take values between 0 and 1, we selected it as prior for \(\theta\). Furthermore, the beta distribution has flexible shapes, which is not the case of a standard uniform distribution. Selecting beta as prior distribution for \(\theta\) restricts its values, which are in fact delimited by the nature of the Ndfa concept to be \(0\le \theta \le 1\). This exemplifies how priors can behave as regulators in Bayesian models [18].

The hyperparameters for the beta distribution used in Eq. 10 for \(\theta\) were defined based on previous literature to best represent our prior knowledge of that parameter. However, no information was directly available for the \(\theta\). Thus, bringing Eq. 4 and Eq. 6 and considering that \(\theta\) represents the Ndfa value when PNB (or TNB) is equal to zero:

This result indicates that the PNB equals zero when the Ndfa is equal to the N harvest index or NHI [3, 4]. This calculation uses PNB rather than TNB because most current scientific literature calculates NHI without considering below-ground biomass contribution.

We conducted a literature review to collect information about the NHI of the nine legumes species included in this study. This review was independent from that utilized by [13]. The literature search was conducted through Google Scholar^®, Scopus^®, and Web of Science^® search engines (last search on August 8, 2023) using the following keywords: (“legume scientific name” OR “legume vulgar names”) AND (“nitrogen harvest index” OR “NHI” OR “N harvest index”). We retrieved a total of 153 articles (excluding duplicates). The selection criteria were: (i) the experiments were performed in field conditions; (ii) NHI has been reported, and calculated excluding roots; and (iii) management information (e.g., N rate, sowing date, irrigation, insect, and pest management) and potential stress factors (e.g., drought, heat, nutrient deficiency) were reported. If the crop performance was severely affected by management practices or stress, the study was not included to avoid NHI values < 0 or > 1. In addition, the study must not have been included in the previous review process used to build the original database to ensure data independence to build the priors for \({\theta }_{PNB}\) and \({\theta }_{TNB}\). Ultimately, out of the pooled of articles, a total of 42 studies were included in the analysis (https://figshare.com/s/60a9cf527ecb9de02166).

We used the NHI values collected for each species to calculate its mean and variance, which represent the mean and the variance of the Ndfa required for a neutral PNB, herein termed as \({\theta }_{PNB}\). Then, the mean and the variance were used to calculate the parameters (\(\alpha\) and β) of the beta distribution via moment matching (Supplementary Note 2), which was used as prior distribution for each of the studied species (Table 2). For the Ndfa to achieve a neutral TNB, we reduced the expected value of the Ndfa in a proportion equivalent to the proportion of N that is allocated to root according to previous information [13, 21]. Given the low certainty of this prior information, we increased the variance of the prior distribution by 50% to account for this uncertainty. Finally, we used the recalculated mean and variance to calculate the hyperparameters of the beta distribution for \(\theta\), now referred as \({\theta }_{TNB}\) (Table 2). Supplementary Fig. 1 illustrates the discrepancies between prior probability distributions of \({\theta }_{PNB}\) and \({\theta }_{TNB}\).

Model fitting and parameters of the posterior probability distributions

The model presented in Eq. 8 to Eq. 11 was fitted to the nine species in the original database [13] for both response variables (PNB and TNB). The expected value and variance of the model parameters (\({\beta }_{1}, \theta ,\) and \(\sigma\)) were computed from their marginal posterior probability distributions (Table 1; Supplementary Note 1) for the PNB and TNB. Subsequently, we used the estimated expected values and variances to determine the parameters of the probability distribution of \({\beta }_{1}, \theta ,\) and \(\sigma\) via moment matching (Supplementary Note 2). Those parameters are reported in Table 3, facilitating their use as priors in future applications of the method presented in this study.

Case study

In this section, we bring and describe a case study to showcase a potential use of the method presented in this article. This illustration is applied after estimating \(\theta\), and quantifying its uncertainty, to formally determine whether the PNB underestimates the true N balance in legume species. The first step is computing the PNB and TNB using independent observations. Then, these observed PNB and TNB are used to fit the Bayesian model presented in Eqs.8–11. Once the model is fitted, the posterior probability distribution for \({\theta }_{PNB}\) and \({\theta }_{TNB}\) are selected. The Ndfa comparison is made simply by subtracting the posterior probability distribution for \({\theta }_{PNB}\) and \({\theta }_{TNB}\) parameters. Then the quantiles of the desired credible interval are computed. Finally, it is observed whether zero is included in the credible interval of the distribution of the difference: (i) if zero is included, we conclude \({\theta }_{PNB}\) and \({\theta }_{TNB}\) are not different, (ii) if zero is not included, \({\theta }_{PNB}\) and \({\theta }_{TNB}\) are different.

For simplicity, we implemented this case study only for two species, chickpea, and common bean, using data from a literature review [13]. Before fitting the model, we split the data into half by randomly sampling the collected studies (without replacement), which resulted in five chickpea and two common bean studies per subset. Then PNB and TNB were computed in each subset independently. The data was split to make comparisons between \({\theta }_{PNB}\) and \({\theta }_{TNB}\). Next, we fitted the Bayesian model (Eq. 8 to Eq. 11) to these subsets within each species. The posterior probability distribution for \({\theta }_{PNB}\) and \({\theta }_{TNB}\) were obtained and subtracted. The 95% credible interval was determined by computing the 0.025 and 0.975 quantiles of the probability distribution of the difference. Finally, it was observed whether zero was included in the credible interval.

Computation and reproducibility

The Bayesian model presented in Eq. 8 to Eq. 11 was fitted using a Markov Chain Monte Carlo (MCMC) algorithm called Non-U-Turn Sampling (NUTS). A total of 4 chains were implemented with 20,000 iterations in total and 10,000 iterations as warm-up. The convergence of the chains was assessed visually through trace plots and analytically via the Gelman-Rubic diagnostic [22]. A seed was set for reproducibility. We performed the Bayesian analyses using Stan probabilistic programming language via rstan package [23]. The bootstrapping technique was implemented using the rsample package [24], while the delta method was carried out with the msm package [25]. All the statistical analyses were performed using the R software [26] in RStudio interface [27]. The code for the analyses is publicly available in https://github.com/FranciscoPalmero/Ndfa_uncertainty and https://figshare.com/s/60a9cf527ecb9de02166. The databases used in this article are available at https://figshare.com/s/60a9cf527ecb9de02166.